Animal Crossing New Horizons: A New Birthday Problem
In a room of 23 people, what’s the probability that at least two of them will share the same birthday? The answer is around 50%, a lot more than people usually expect.
This is an example of the classic Birthday Problem. The trick to calculating it is to start by calculating the complement, - i.e. the probability that no one in the room shares the same birthday. Then, this probability is subtracted from 1:
(I won’t go into why this works here, as there are already plenty of good explanations out there on the internet).
But, what does this have to do with Animal Crossing New Horizons?
Well, this week’s #TidyTuesday dataset is Animal Crossing themed! Amongst the csvs provided on github, is one called villagers.csv, displaying information about the 391 possible villagers that might move to your island on the game.
This dataset helpfully includes each villager’s birthday - after all, you wouldn’t want to be the kind of neighbour who forgot another villager’s birthday, now would you?
villagers %>%
head(10)## # A tibble: 10 x 11
## row_n id name gender species birthday personality song phrase full_id
## <dbl> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr>
## 1 2 admi~ Admi~ male bird 1-27 cranky Stee~ aye a~ villag~
## 2 3 agen~ Agen~ female squirr~ 7-2 peppy DJ K~ sidek~ villag~
## 3 4 agnes Agnes female pig 4-21 uchi K.K.~ snuff~ villag~
## 4 6 al Al male gorilla 10-18 lazy Stee~ Ayyee~ villag~
## 5 7 alfo~ Alfo~ male alliga~ 6-9 lazy Fore~ it'sa~ villag~
## 6 8 alice Alice female koala 8-19 normal Surf~ guvnor villag~
## 7 9 alli Alli female alliga~ 11-8 snooty K.K.~ graaa~ villag~
## 8 10 amel~ Amel~ female eagle 11-19 snooty K.K.~ eaglet villag~
## 9 11 anab~ Anab~ female anteat~ 2-16 peppy Aloh~ snorty villag~
## 10 13 anch~ Anch~ male bird 3-4 lazy K.K.~ chuurp villag~
## # ... with 1 more variable: url <chr>Now, seeing as there are 365 possible birthdays (or 366 on a leap year), and 391 villagers, solving the Birthday Problem is incredibly easy for this dataset. There’s no possible way for some villagers not to wind up sharing a birthday!
We can confirm that some villagers share birthdays by counting the number of dates that appear more than once in birthdays:
villagers %>%
count(birthday, sort = TRUE) %>%
filter(n > 1) %>%
head(10)## # A tibble: 10 x 2
## birthday n
## <chr> <int>
## 1 1-27 2
## 2 10-1 2
## 3 10-12 2
## 4 10-13 2
## 5 10-15 2
## 6 10-21 2
## 7 10-24 2
## 8 10-6 2
## 9 12-1 2
## 10 12-29 2There are 30 dates that appear more than once. We can also see that the total number of villagers sharing a birthday never exceeds two. This means that, in our villagers dataset, there are 60 villagers who share a birthday with another villager.
We can see this clearly by plotting the number of birtdays per date in a tileplot:
all_dates <- tibble(days = seq(as.Date("2002-01-01"), as.Date("2002-12-31"), "days"))
# prepare data for calendar plot
bday_per_date <- villagers %>%
mutate(birthday = lubridate::ymd(paste("2002", birthday, sep = "-"))) %>%
count(birthday) %>%
right_join(all_dates, by = c("birthday" = "days")) %>%
mutate(n = ifelse(is.na(n), 0, n)) %>%
rename(num_villagers = "n", date = "birthday") %>%
mutate(month = lubridate::month(date, abbr = TRUE, label = TRUE)) %>%
mutate(monthday = lubridate::day(date)) %>%
mutate(week = as.numeric(format(date, "%W"))) %>%
mutate(weekday = factor(weekdays(date, abbreviate = TRUE),
ordered = TRUE,
levels = c("Sat", "Fri", "Thu", "Wed", "Tue", "Mon", "Sun"))) %>%
group_by(month) %>%
mutate(monthweek = 1 + week - min(week))
# calendar tile plot
bday_per_date %>%
ggplot(aes(monthweek, weekday, fill = num_villagers)) +
geom_tile(colour = "gray98", alpha = 0.9) +
geom_text(aes(label = monthday), size = 2.5, alpha = 0.9, colour = "gray20") +
facet_wrap(~month) +
labs(x = "Week of Month",
y = "",
fill = "No. of Birthdays",
title = "Animal Crossing Villager Birthdays") +
theme(text = element_text(family = "Arial Nova"),
panel.background = element_rect(fill = "gray98"),
panel.grid = element_blank(),
legend.text = element_text(size = 8),
legend.title = element_text(size = 10, colour = "gray10"),
axis.title = element_text(colour = "gray10"),
plot.title = element_text(size = 14),
strip.background = element_rect(fill = "#cff5f5")) +
scale_fill_gradient(low = "#FFC371", high = "#FF5F6D", breaks = c(0, 1, 2)) 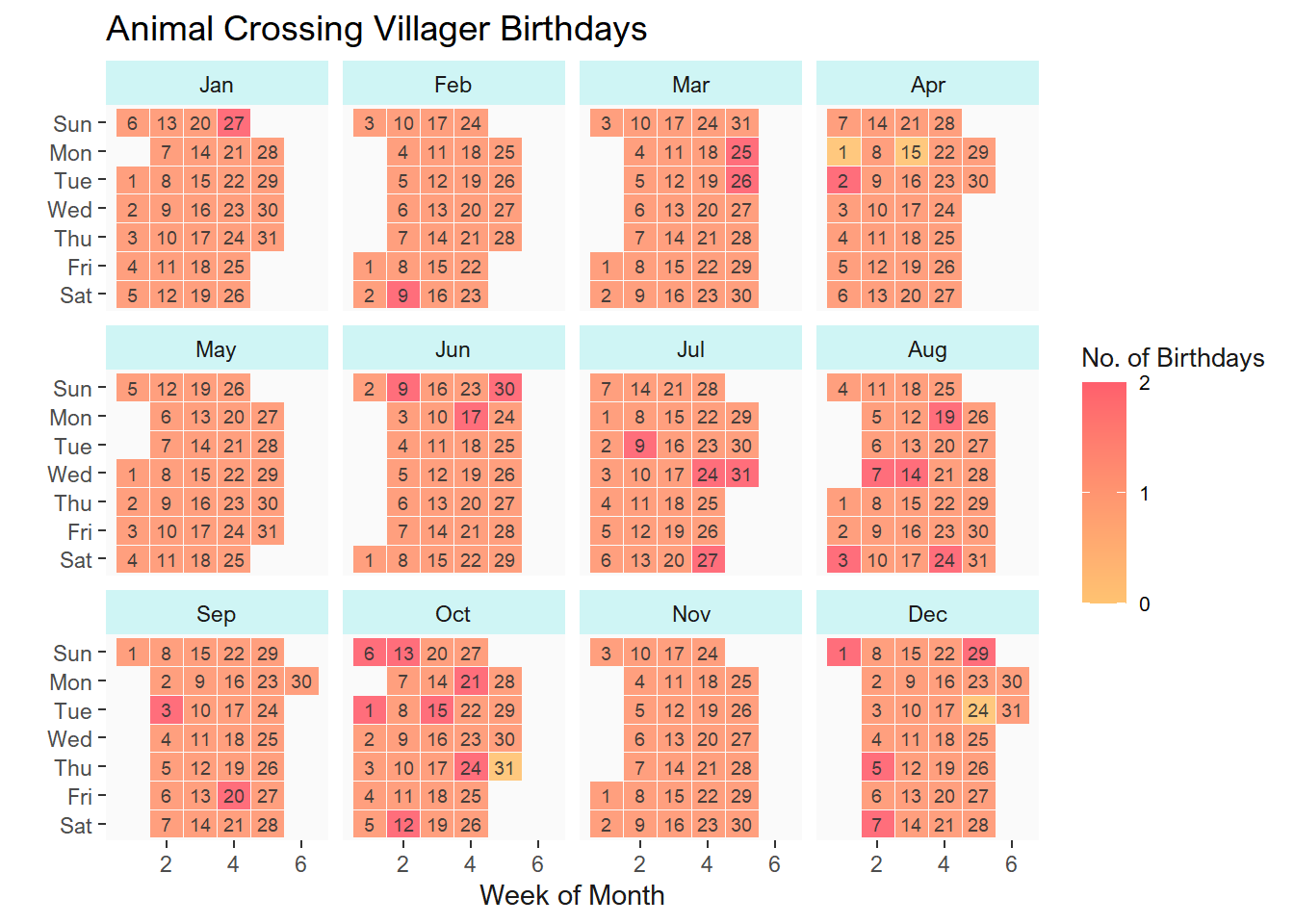
So, there are 30 non-unique birthday dates, and 60 villagers share a birthday with another villager, meaning that no more than two villagers share a birthday. Hmmm…
Now, I have every reason to suspect that the birthday date allocation is not random in animal crossing. I imagine the game makers will have tried to avoid having multiple villagers on the same island with the same birthday. The fact that we never see more than two villagers with the same birthday definitely seems to corroborate this.
Nonetheless, it does lead to an interesting question: if the birthday dates of the villagers were set randomly and independently, how likely would we be to get just 60 villagers with a shared birthday? And, how many of the 391 villagers would we, on average, expect to see share a birthday?
I tried looking up existing solutions to this, and didn’t get very far. It basically looks to a) be complicated and b) involve some very big numbers.
But, there’s a much simpler approach available! Instead of trying to find an exact solution, we can use simulated data.
First, we need a function that randomly generates a birthday date from one of the 365 days of the year, for each of our 391 Animal Crossing villagers.
days <- seq(from = 1, to = 365, by = 1)
sample_birthdays <- function() {
sample_dates <- sample(days, 391, replace=TRUE)
count_dates <- table(sample_dates)
return(sum(count_dates[count_dates > 1]))
}The function I’ve created here randomly samples from the numbers 1-365 with replacement 391 times, and returns the total number of duplicate data points (corresponding to our villagers who share a birthday with someone else).
Next, we need to run the function multiple times to generate a large number of samples. Here, I use the replicate() function to generate 50,000 samples.
set.seed(2025)
num_sharing_villagers <- replicate(50000, sample_birthdays())
obs_duplicates <- tibble(sample_num = seq(1:50000),
num_sharing_villagers = num_sharing_villagers)If only all data collection were this simple.
Finally, we can plot a histogram showing the number of villagers sharing a birthday across all 50,000 samples.
obs_duplicates %>%
ggplot() +
geom_histogram(aes(num_sharing_villagers),
alpha = 0.8,
fill = "#FFC371",
bins = 30) +
labs(x = "Number of Villagers With a Shared Birthday",
y = "Frequency") +
theme_minimal() +
theme(text = element_text(family = "Arial Nova"),
axis.title.x = element_text(vjust = -0.2, colour = "gray10"),
axis.title.y = element_text(vjust = 1.2, colour = "gray10")) +
geom_vline(xintercept = 257, linetype = "dashed", size = 1, colour = "gray75")
The simulated data shows us that on average, we would expect roughly 257 villagers to share a birthday with another villager.
As for the mere 60 sharing villagers in the actual Animal Crossing dataset? Well, across 50,000 samples, I didn’t get a number as small as 60 even once. So that’s looking… very unlikely by chance.
Conclusion? These Animal Crossing villagers really need to learn how to share more.
Final fun fact: I just looked up whether I share my birthday with a villager. Apparently I share my birthday with Kevin, a male chauvinist jock pig, whose catchphrase is apparently “weeweewee”. Great.